ผู้ช่วยศาสตราจารย์ ดร.วรวิทย์ จันทร์สุวรรณ
ปรับปรุงล่าสุด : 14 สิงหาคม 2561

การทดสอบทีโดยโปรแกรม Excel เป็นการประยุกต์ใช้โปรแกรมไมโครซอฟต์เอกซ์เซล (Microsoft Excel) ทดสอบทางสถิติในการทดสอบที (t-test) แบบ dependent เป็นการทดสอบข้อมูลของกลุ่มตัวอย่างที่ไม่เป็นอิสระจากกัน หรือเรียกว่า เป็นการทดสอบที (t-test) แบบจับคู่ หรือ Paired t-test
โดยข้อมูลที่ได้มาจากกลุ่มตัวอย่างเดียวกัน เช่น เปรียบเทียบผลการทดสอบก่อนเรียนและผลการสอบหลังเรียนของผู้เรียนกลุ่มเดียวกัน ว่าแตกต่างกันอย่างมีนัยสำคัญทางสถิติหรือไม่
การติดตั้งเครื่องมือ Add-in
การทดสอบทีโดย MS Excel ใช้ซอฟต์แวร์ไมโครซอฟต์เอกซ์เซล (Excel) ช่วยในการคำนวณค่าต่างๆ สามารถทำให้การคำนวณนั้นสามารถทำได้ง่ายขึ้นและใช้เวลาน้อยลง และยังสามารถลดการผิดพลาดจากการคำนวณได้ ฟังก์ชันสำหรับการคำนวณใน Excel มีจำนวนมากและเราสามารถเลือกให้ถูกต้องกับผลที่เราต้องการวิเคราะห์
การประเมินผลโดยการเปรียบเทียบผลการวิเคราะห์ของทั้ง 2 วิธี ในการทดสอบความแตกต่างแบบจับคู่ โดยแต่ละคู่มีความสัมพันธ์กันนั้น ซึ่งสามารถทำได้โดยการใช้โปรแกรม Excel ในที่นี้จะขอยกตัวอย่างการคำนวณด้วย Excel รุ่น 2016 ตามขั้นตอนดังนี้
1. เปิดโปรแกรม Excel (เลือกแถบ Data ดูว่ามีไอคอน Data Analysis ปรากฎหรือไม่

2. ถ้าไม่มี Tool สำหรับการคำนวณทางสถิติ ให้เพิ่มเครื่องมือเข้าไปดังนี้ เลือก File > Options > Add-Ins เลือกแถบ Analysis ToolPak-VBA แล้วเลือก Excel Add-Ins ในช่องด้านล่าง กด Go
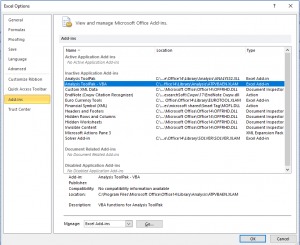
3. ปรากฏหน้า Add-Ins ดังรูป ให้เลือก P หน้า Analysis ToolPak และ Analysis ToolPak-VBA แล้วกด OK
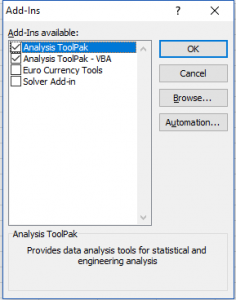
แถบ Data จะมีไอคอน Data Analysis ปรากฎ

การวิเคราะห์ค่า T-test ด้วย Excel ก่อนจะทำการทดสอบ ต้องมีการตั้งสมมุติฐานก่อน
- สมมติฐานว่าง (null hypothesis) เขียนแทนด้วยสัญลักษณ์ H0 เป็นสมมติฐานที่แสดงว่าจะไม่มีการเปลี่ยนแปลงใด ๆ ไม่มีความแตกต่าง หรือความแตกต่างเป็นศูนย์ จึงมักแทนด้วยเครื่องหมาย =, ≤, ≥
ดังนั้นในตัวอย่างนี้คือ ค่าเฉลี่ยของวิธีพัฒนาขึ้นและวิธีมาตรฐานแตกต่างกันอย่างไม่มีนัยสำคัญ - สมมติฐานทางเลือก (alternative hypothesis) เขียนแทนด้วยสัญลักษณ์ Ha เป็นสมมติฐานที่ตั้งขึ้นมาเพื่อขัดแย้ง H0 เป็นสมมติฐานที่แสดงการเปลี่ยนแปลงมีความแตกต่าง จึงแทนด้วยเครื่องหมาย ≠, <, >
ดังนั้นในตัวอย่างนี้คือคือ ค่าเฉลี่ยของวิธีพัฒนาขึ้นและวิธีมาตรฐานแตกต่างกันอย่างมีนัยสำคัญ
หมายเหตุ: การกำหนดสมมุติฐานว่า จะเป็น One-tailed test หรือ Two-tail test ขึ้นอยู่กับการศึกษาข้อมูลพื้นฐานที่เกี่ยวกับเรื่องนั้น ๆ ตลอดจนเจตคติของผู้วิจัย ถ้าไม่แน่ใจว่าผลจะออกมาเป็นอย่างไร อาจจะเป็นไปได้ทั้งทางมากหรือทางน้อย เป็นต้น ในลักษณะนี้ ควรกำหนดไว้เป็น Two-tail test แต่ถ้าค่อนข้างแน่ใจ จากการศึกษามาแล้วว่าผลที่ได้อาจจะมากกว่าหรือน้อยกว่าอย่างแน่นอน ก็สามารถกำหนดเป็นลักษณะ One-tail test ได้
การทดสอบทีแบบจับคู่ (paired t-test)
ทำการป้อนข้อมูลที่ต้องการประมวลผลการทดสอบความแตกต่างแบบจับคู่ โดยแต่ละคู่มีความสัมพันธ์กัน (Paired t-test) ดังนี้
1. เลือกแถบ Data > Data Analysis ปรากฏหน้า Data Analysis เลือก t-Test : Paired Two-Sample for Means แล้วกด OK
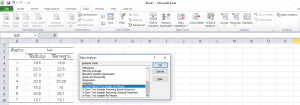
2. ปรากฏหน้า t-Test : Paired Two Sample for Means ดังรูป
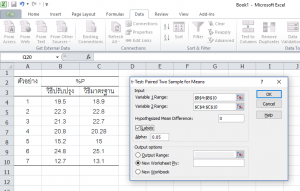
ในส่วนของ Input
Variable 1 Range: ให้เลือกช่วงของข้อมูลชุดที่ 1 สำหรับวิธีปรับปรุง (จากตัวอย่างนี้คือ B4-B10)
Variable 2 Range: ให้เลือกช่วงของข้อมูลชุดที่ 2 สำหรับวิธีมาตรฐาน (จากตัวอย่างนี้คือ C4-C10)
ช่อง Hypothesized Mean Difference ให้ใส่ 0
เลือก P หน้า Labels เพราะมีการรวมชื่อตัวแปรไว้ในช่วงของข้อมูล
Alpha: 0.05 หมายถึงระดับนัยสำคัญทางสถิติที่ต้องการ (95%)
ในส่วนของ Output options
ช่อง O ให้เลือก New Worksheet Ply: เมื่อโปรแกรมคำนวณเสร็จจะนำผลที่ได้ไปไว้ใน Worksheet ใหม่ หรือเลือก Output Range และใส่ช่วงที่จะบันทึกผลลัพธ์ที่จะเกิดขึ้น
กด OK
3. ผลการวิเคราะห์จะได้ตาราง t-Test : Paired Two-Sample for Means ดังรูป
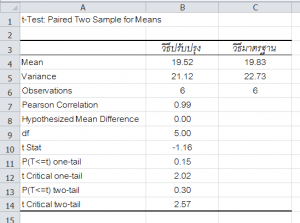
การแปรผล
- ถ้าค่า t-Stat ที่ได้ น้อยกว่า ค่า t-Critical แสดงว่า เราไม่อาจปฏิเสธ Null Hypothesis
- ถ้าค่า t-Stat ที่ได้ มากกว่าหรือเท่ากับ ค่า t-Critical แสดงว่า เราปฏิเสธ Null Hypothesis และ ยอมรับ Alternative Hypothesis
- ถ้าค่า P มากกว่าค่าระดับความเชื่อมั่น ตามที่กำหนด แสดงว่า เราไม่อาจปฏิเสธ Null Hypothesis
- ถ้าค่า P น้อยกว่าหรือเท่ากับค่าระดับความเชื่อมั่น ตามที่กำหนด แสดงว่า เราปฏิเสธ Null Hypothesis และยอมรับ Alternative Hypothesis
จากตัวอย่าง พิจารณาได้ 2 วิธี ดังนี้
- พิจารณาจากค่าค่า t-Stat (-1.16) ซึ่งน้อยกว่าค่า t Critical two-tail = 2.57 จึงเป็นการยอมรับสมมติฐานหลัก และปฏิเสธสมมติฐานรอง นั่นคือ ค่าเฉลี่ยของผลการวิเคราะห์ทั้ง 2 วิธีแตกต่างกันอย่างไม่มีนัยสำคัญ
- พิจารณาจากค่า P-value [P(T<=t) two-tail] (0.30) มีค่ามากกว่า 0.05 กล่าวคือ p>0.05 ดังนั้น จึงยอมรับสมมติฐานหลัก และปฏิเสธสมมติฐานรอง
สรุป ค่าเฉลี่ยของผลการวิเคราะห์ทั้ง 2 วิธีแตกต่างกันอย่างไม่มีนัยสำคัญ
